A few weeks ago I got an urge to build a calculator parser and evaluator. Something that can take a simple 5 + 6 + 7 expression and evaluate it to a number: 18.

I had never worked with calculator parsers before and had also never heard of the shunting-yard algorithm when I wrote this. I wanted to go in blind just for the fun of it and to see what I could come up with.

With all that said, let’s jump right in.

Defining what we’ll parse

Calculator parsing encompasses a LOT of different functionalities depending on the type of calculator you have. Handling every possible interaction would be quite tedious, so I only included ones that were either:

• Basic functionality
• Added something different and fun

This is the initial list of functionality I decided to work with:

• Raw integers (no floating point operations)
• + (addition)
• - (subtraction)
• / (division)
• * (multiplication)
• ** (powerOf)
• () (nested sub-expressions, parenthesis)
• And only accept numbers smaller than Scala signed int type

And yes, the final point does mean it’s being written in Scala (not rust!!). I decided it would be a good opportunity to learn a new language.

The making of our multi-pass parser/interpreter

Now that we’ve defined a subset of functionality our parser will take, let’s discuss design. With my knowledge of basic compiler theory, the goal was to mimic a simple multi pass compiler. What I came up with wasn’t exactly the same, but it was quite close. Here are the steps I came up with:

Receiving the source expression

This is the simplest one, the user provides us with a string like so:

5 + 6 + 7

That’s all there is to it.

Tokenization

Now we must convert the characters in the string into tokens. These are easier to work with than raw strings, and remove all unnecessary characers (like whitespace) leaving us with less to deal with. It also gives them a little typing information.

Example tokenization:

5 + 6 + 7 => List(Literal(5), Addition(), Literal(6), Addition(), Literal(7))

During this stage I decided to nest parenthesis in sublists so they would be able to circumvent handling order of operation when handling their subtree. This was intentional even though it added a little extra work in this one phase. I didn’t want any of the one phases doing too much, so I figured this was a reasonable tradeoff for adding a bit of complexity to the tokenizer.

This means the tokenizer is also responsible for ensuring parenthesis were well balanced in addition tokenizing strings.

In retrospect, if I were rewriting my parser now I think the proper way to handle this would be to add a pass in between after this step finished and before the next one, but I digress.

When parenthesis were passed in, the result would look like so:

5 + (6 + 7) => List(Literal(5), Addition(), Parenthesis(Literal(6), Addition(), Literal(7)))

The inner workings of the tokenizer

The short gist of how the tokenizer works is quite simple. We loop over all of the characters in the string we’re given and build tokens for each one. If we get 2 numbers in a row, we keep building the literal we have (e.g. Literal(5) when we receive 6 as the next character becomes Literal(56)) and receiving a second multiplication sign turns the Multiplication() into a PowerOf().

All whitespace is skipped.

The most complicated part of tokenizing is handling parenthesis. When handling parenthesis we recursively call our tokenizer, popping a parenthesis on the stack and handling all subexpressions.

We stop handling sub-expressions when we receive a close parenthesis. When receiving a close parenthesis, we tell the parent to ignore all characters up to the range of the final close parenthesis we got in the child. In doing so, we are able to recursively handle any number of parenthesis without trouble.

AST building

The next step is building an AST that handles order of operations I ended up redesigning this part a number of times until I got it just right.

The AST builder does just that, it turns a list of tokens into a simple AST sort of like so:

List(Literal(5), Addition(), Literal(6), Addition(), Literal(7)) => Node(Addition, Node(Addition, Literal(5), Literal(6)), Node(Literal(7)))

In addition to building an AST, the other goal of the AST builder is to represent nodes in a form that respects order of operations. Each node type is given a priority which decides how to place the child, and whether or not to re-parent (more on that in the inner workings part).

We can get around order of operations for parenthesis by handling them in their own recursive call and placing them in a parenthesis block. This way everything inside of the parenthesis block gets order of operations, but is totally ignored outside of it.

This AST might look good enough to be the final AST, but it is very different. All branches are optional and nothing is validated. Literals are allowed to have children if a list of tokens were somehow passed through with one literal after another. Arguably without error handling though, this would be a fine final AST representation.

This form is best represented as: Nodes with type tags, but the typing is totally unchecked.

The inner workings of the AST builder

In the below section there are a number of diagrams with colors, this is the key for what each color means:

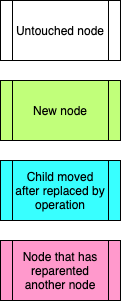
The AST builder starts simple. We start by making the first node the root. Once we receive the second node, we re-parent the root to the second node (making the assumption it is an operation) and making the old root the left hand side. Finally, the third node is right hand side (making the assumption again it is a literal).

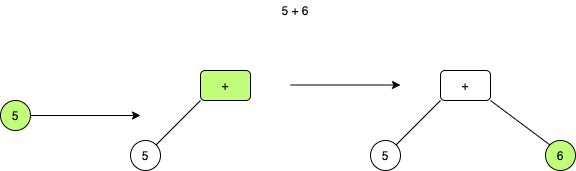
But what happens when you get a fourth node? And then a fifth? Let’s look at how we’d handle it. Say we were working with: 5 - 7 * 2 Order matters a lot here. If we do not respect order of operations, we’re going to get -4 instead of -9. That’s no good!

With a bit of magic of: knowing how I will have the interpreter run later, I know nodes deepest in the tree will be evaluated earlier than nodes deeper in the tree, and so the following design tries to get actions that must run first to become nodes that are hidden deep in the tree.

For this to happen properly, we need a convenient and consistent way to re-parent nodes. We already re-parented once with the root node, so let’s ensure we can do it with every other node.

In order to make this happen, each node type is given a priority:

• Literal => 1
• Parenthesis => 1
• PowerOf => 2
• Multiplication => 3
• Division => 3
• Addition => 4
• Subtraction => 4

With these numbers down, we can now follow the system of: if the current node’s priority is higher or equal to the last node’s priority, we will re-parent it and make the last node, the left hand side child.

It is important we check equal to in addition to higher than, because not all expressions are associative. 3 - 4 - 5 must reparent ensuring 3 - 4 is run first, otherwise the result will be incorrect.

With that said, it’s also important to remember in a valid expression operations only come on every odd token. So the eventh token is always put on the left hand side, and we will only consider re-parenting when working with numbered tokens.

Likewise, if we do not re-parent the operation, we do end up re-parenting a literal. In our current system, by the time we get to where we would consider re-parenting an operation, that operation is already fully hydrated (both children are values of some sort).

This is quite confusing to explain and is easier done with two diagrams:

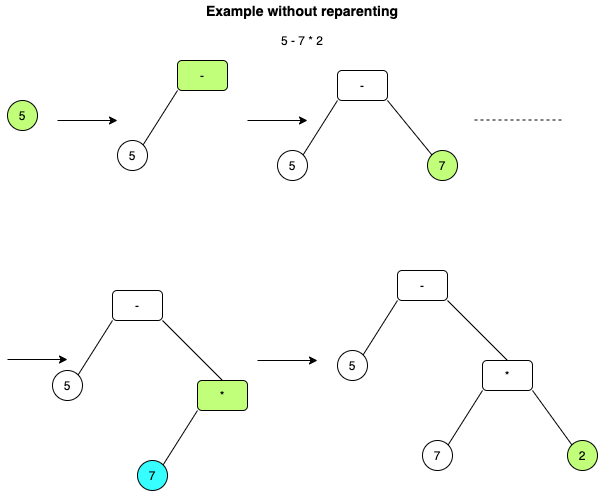
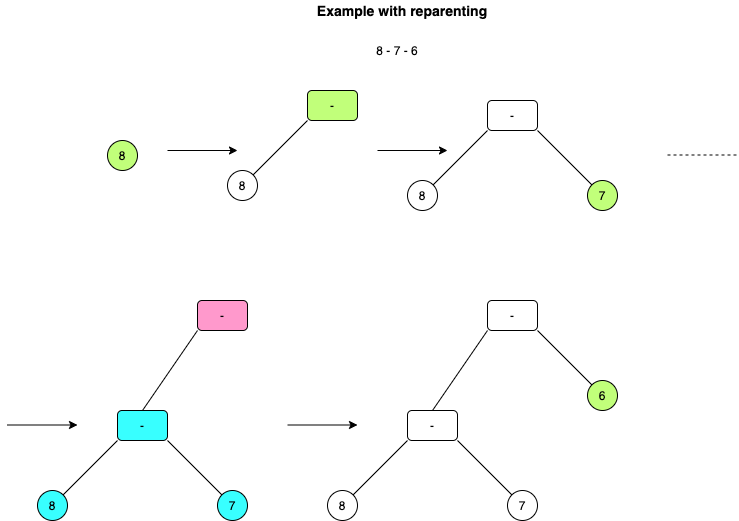
The AST validator

This is the final step before we’re allowed to evaluate anything. Here we walk through the tree we’ve made and validate all of the building we’ve done so far. Here we check and see things like: operations must have two children and literals must have no children.

As we validate, we remove all optionals from the tree and are left with a tree we know is valid. At this point we are basically done.

The interpreter

Now that we have an AST, this part is quite easy. There isn’t much work that has to be done here.

We just require each node to have an eval function:

1
2
3

trait Pattern {
  def eval: Int
}

And then to evaluate, all we have to do is call eval and either:

• If we are a literal, return the self value
• If we are an operation, return (left hand side).eval ${OPERATION} (right hand side).eval
• If we are parenthesis, call (inner expression).eval

This recursive call will get us an answer guaranteed every time.

And that’s it

If you’ve got this far, you should now have a pretty solid idea of how my homebrew calculator parser library works. It is not faster than the shunting-yard algorithm, but it was certainly fun to make.

If you’re interested in seeing the code for yourself, you can look at the repo here.